Boston ACS Meeting 2002

back to e-Publications

INTRODUCTION

The meeting was the fourth largest in ACS history, with more than 17,000 registrants. Just under 7000 papers were presented; 309 companies exhibited in 490 booths. This report concerns mainly the Exhibition and the technical sessions of CINF (the Division of Chemical Information) and COMP (the Division of Computers in Chemistry). To make the report more useful, I am including some news unrelated to the ACS meeting. I have used press releases dated up to December 31, 2002.

NEWS, NEW PRODUCTS AND THE EXHIBITION

<Clip>>

Accelrys

Corporate news

Pharmacopeia, Accelrys’ parent, has restructured its business in response to market conditions. As part of the restructuring, the company is reducing its staff by approximately 80 employees, a reduction of approximately 10%. Management estimates this action will reduce operating expenses by approximately $8.0 million in a year, principally from lower selling, general and administrative expenses of the company’s software operations.

Accelrys has opened its new European headquarters in Cambridge, England. The headquarters will be the base for Accelrys’ European operations, and will provide services, support and training to its UK and European customers. The 42,000 square foot offices will house product development, marketing, sales, finance, and administration functions. It will be used to help strengthen existing relationships with the academic and business community in the UK as a whole and the Cambridge region in particular. As part of this programme, the offices hold a purpose-built meeting suite that will support a variety of scientific conferences and seminars, as well as customer training activities. To help promote scientific networking, these facilities will be opened to collaborators and partner organisations.

Mark J. Emkjer has been appointed President of Accelrys. Mr. Emkjer brings more than twenty years of management experience to Accelrys, most recently as President and Chief Operating Officer of Sunquest Information Systems. Prior to joining Sunquest, Mark was President and Chief Executive Officer of Pace Health Management Systems, a provider of clinical decision support software. Emkjer replaces Michael Stapleton, who resigned on December 31.

Accelrys will host AccelrysWorld, an international conference to address scientific and IT solutions in the pharmaceutical, biotechnology, chemicals, and other research-based industries, taking place on February 24-26, 2003 at the Hotel del Coronado in San Diego, California.

Customers

Accelrys has announced a software licensing agreement with NiKem Research, the new chemical technology company spun off from GlaxoSmithKline. Under the terms of the agreement, Accelrys has licensed the use of its Cerius² and Catalyst suites. The Cerius² and Catalyst suites were chosen to complement existing computational capabilities at NiKem Research, particularly for their ability to support library optimisation and pharmacophore generation. It will help NiKem’s researchers to construct their new OptiLead Platform.

Accelrys has signed a global software agreement with Syngenta under the terms of which Syngenta gains enhanced access to Accelrys modelling tools and will use Accelrys technology to construct an enterprise cheminformatics system The agreement covers Syngenta sites worldwide. Syngenta is already a user of Accelrys technology in the area of modelling of chemical and biological systems. The new agreement expands this use and enables Syngenta to apply Accelrys cheminformatics tools.

AstraZeneca has renewed its unified global licensing agreement with Accelrys. Scientists at 10 of the company’s sites worldwide will continue to use Accelrys’ modelling and simulation software to characterise therapeutic targets and to identify and optimise lead compounds.

Digital Gene Technologies has chosen DS SeqStore as a component of its bioinformatics infrastructure. Accelrys has announced a three-year software licensing agreement with Intervet Innovation, part of Akzo Nobel. Accelrys’ molecular modelling, simulation and combinatorial chemistry applications will be deployed in Intervet’s new research centre located in Schwabenheim, near Frankfurt. The new research unit will serve the entire Intervet organisation, providing all computational tools required for drug design.

Partners

Agilent Technologies and Accelrys have announced a software licensing agreement and technology alliance under the terms of which Agilent will license the use of Accelrys’ Viewer ActiveX Control for 3D visualization of molecular structures. The Viewer ActiveX Control will be integrated into the recently released Agilent Synapsia Informatics Workbench, and will enable scientists and technicians in the pharmaceutical and biotech industry to visualise and share molecular information. Accelrys’ Viewer ActiveX Control visualisation capabilities will be incorporated into new Agilent informatics software products that will include the following features: protein display styles including C-alpha, ribbon, tube, and schematic; line, stick, ball and stick, scaled ball and stick, CPK, and polyhedron atom display styles; orthographic or perspective viewing projection; and lighting colour, shading, and direction options.

United Devices has announced a joint effort with Accelrys to launch a second phase of the Cancer Research Project in which more than 1.5 million PCs from around the world have been aggregated to help scientists and researchers at Oxford University analyse billions of molecules against selected proteins (see the paper by Davies later in this report). The second phase of the project will use Accelrys’ high-throughput docking and scoring application, Cerius² (C²) LigandFit, running on United Devices’ MetaProcessor platform to refine the research by screening the massive number of “hits” produced in phase one against the original 12 protein targets. By processing the existing research data through the grid-enabled version of C² LigandFit, the project scientists will be able to predict and prioritise more accurately the suitability of the generated “hits” as potential lead candidates for subsequent drug development.

Discovery Studio

Accelrys has introduced more Discovery Studio products: the Accord Enterprise Informatics suite. This suite is a comprehensive solution for the storage and management of corporate chemical, biological screening, and inventory data within life science organisations. It enables discovery organisations to integrate their chemical and biological data into a unified and scalable system.

The main Accord Enterprise Informatics products available include Discovery Studio Enterprise Core, Discovery Studio Accord Chemistry Cartridge, and Discovery Studio Accord BioStore. The first of these is the central component of the suite which delivers knowledge management tools for integrating chemical and biological databases and manipulating the chemical and biological data retrieved from them. Discovery Studio Accord Chemistry Cartridge is the engine that allows Oracle to store, search, and index chemical data in Accord Enterprise Informatics. The cartridge is an integral part of the suite, but is also available to developers to build custom, Oracle-based, cheminformatics solutions. Discovery Studio Accord BioStore is an Oracle-based framework for managing assays, protocols, and test data.

In October, Accelrys announced further applications for the Discovery Studio family of products. DS Modeling is a life science molecular modelling and simulation research environment accessible via Windows-based PCs. It supports both computational specialists and scientists who are new to these technologies. This first release of DS Modeling features functionality focusing on protein characterisation and homology modelling.

DS Modeling is designed for structural and computational biologists and chemists who need to perform expert-level modelling and simulation tasks in an easy-to-learn yet powerful environment. Its graphics, validated science, and experimental “wizard” approach enable sequence and 3D-structure characterisation, visualisation, analysis, and modelling of protein targets. It allows demanding calculations to be run across networks on a range of different servers. DS Modeling interoperates with DS Gene and other Discovery Studio products through DS ProjectKM, integrating data storage and analysis of information from bioinformatics, modelling, and cheminformatics applications.

The DS Modeling components released include DS MODELER, DS CHARMm and DS Modeling Visualizer. DS MODELER is a comparative protein modelling methodology that generates refined 3D homology models of protein sequences from a sequence-structure alignment. DS CHARMm is a wizard-guided tool that enables both beginner and expert modellers to apply CHARMm technology for studying the behaviour and properties of small, drug-like molecules, large molecules such as proteins, and complexes. DS Modeling Visualizer is the visual centrepiece for the suite of products. It integrates sequence, 3D structure, and hierarchical views of data, enabling the performance of molecular modelling and visualisation in an interactive manner on a standard PC.

Later, Accelrys released Discovery Studio SeqStore, an Oracle-based enterprise solution for managing, analysing, and visualising genomic and proteomic sequence data. It provides data management capabilities, a secure environment for research and collaboration, up-to-date sequence data, and integration with the GCG Wisconsin Package. It delivers a unified environment for managing public, proprietary and third-party data that can be integrated with proprietary and third-party analysis applications. As such, the solution provides a single point of access for all of an organisation’s research data, analysis and visualisation tools.

DS SeqStore complements DS Gene, the first Discovery Studio bioinformatics product. Within DS SeqStore users can register new sequences, record analysis results, annotate existing sequences as new discoveries are made, and integrate and manage data from multiple sources in multiple formats. Users can also save multiple versions of sequences and annotations, enhancing collaboration and recording discovery histories for patent purposes. DS SeqStore automatically updates the database as new information becomes available, giving researchers across the organisation access to the most current data.

Materials Science

Accelrys has released Materials Studio 2.2, which features new and improved tools in the polymer, crystallisation and catalysis areas. The client-server architecture of Materials Studio 2.2 allows researchers to create scenarios on Windows-based PCs, perform calculations on dedicated server machines, view the results back on the PC and share this information with colleagues. The Materials Studio portfolio has been enhanced to include Forcite, MesoDyn and X-Cell, which address atomistic, mesoscale and crystallisation issues, respectively. The DMol3 and CASTEP quantum codes are now available on Itanium 2-based HP servers, with other modules to follow in 2003. CASTEP now has the capabilities of calculating the phonon spectrum of a material using linear response, thereby giving access to the thermodynamical properties of materials at the ab initio level for the first time within Materials Studio.

The company has delivered a customised Catalyst Database Management System (CDMS) to Johnson Matthey, enabling scientists at three sites worldwide to collaborate by sharing information associated with the development of new catalysts and their application to chemical problems. Johnson Matthey scientists will use the CDMS for storing and sharing of data associated with homogeneous and heterogeneous catalysts and ligands either developed in laboratories or acquired commercially, including Anchored Homogeneous Catalysts (FibreCat). The application of these catalysts in the development of new or improved chemical processes is similarly managed by the system, part of which assists in the optimisation of reaction conditions. The system also provides information about the patent position of the products developed within the company. Accelrys Consulting developed the solution in collaboration with a group of Johnson Matthey scientists in the UK.

<Clip>>

CINF AND COMP TECHNICAL PROGRAMMES

<Clip>>

CINF/COMP/MEDI Symposium. Virtual High Throughput Screening, Fast Docking, and Scoring

<Clip>>

Re-optimisation of MDL keys for use in drug discovery
Keith T Taylor, Joseph L. Durant Jr., Burton A Leland, Douglas R Henry, and James G Nourse, MDL Information Systems, 14600 Catalina Street, San Leandro, CA 94577, keitht@mdli.com

(This work has now been published in Durant, J. L.; Leland, B. A.; Henry, D. R.; Nourse, J. G. Re-optimisation of MDL keys for use in drug discovery. J. Chem. Inf. Comput. Sci. 2002, 42, 1273-1280.)

In this work, the following definitions are used. A “descriptor” refers to a molecular feature. Descriptors can be encoded into binary “keybits”. There can be a one-to-one relationship between descriptors and keybits, or hashing can be used to create a many-to-one or many-to-many relationship between descriptors and keybits. An ordered collection of keybits constitutes a “keyset”. “Keys” is context-sensitive and is used to refer to either keybits or ketsets. For ethanoic acid, 27 keys are set.

MDL’s keysets were optimised for substructure searching and were constructed to minimise memory and storage requirements but they do work remarkably well for clustering and diversity analysis, comparable with keysets based on feature trees. There are two common MDL keysets, one containing 960 keybits and the other containing a subset of 166 keybits.

A keybit is defined by nine numbers, n1 through n9. The first four numbers encode various atom, bond, and custom properties into descriptors. The remaining five numbers determine which keybits are set by the descriptor. The MDL algorithm perceives 26 properties of type P, and 30 properties of type A, these being properties such as “halogen” or “atom with more than one chain bond”. Additionally, 32 one-atom environments, such as C(NNN) or C(COO), are perceived.

One class of possible atom-based descriptors results from the presence of one or two properties of type A located on a single atom. For this class, n1=0, while n2 and n3 encode the appropriate values (0-31) of A. A second class results from the presence of an atom with property P, separated by one to four bonds from a second atom with a property P', For this class, n1 encodes the number of bonds between the atoms and n2 and n3 encode the appropriate values of P and P' (a value between 0-31, although not all integers are used). A third class results from the presence of an atom with property A located in the centre of a particular atom environment. In this case n1=7, n2 encodes the atom environment, and n3 encodes the property A.

Another block of descriptors encodes one of 264 atom-bond-atom combinations. These descriptors have n1=6, while n2 and n3 have various values from 4-31 depending on the atoms and bonds involved. Yet another block, with n1=5, encodes a number of custom features. The first sub-block of these descriptors encodes a series of properties (e.g., five-membered ring) which are used in the 166-bit MDL keyset. The next sub-block of 256 encodes atom types 1-256. A final sub-block encodes a variety of MDL Sgroup properties. An Sgroup is defined as structure-differentiating information that is associated with certain atoms, bonds, or fragments in a structure. Examples include polymer and mixture definitions, and so-called data sgroups, that can be arbitrary text or numeric data associated with a collection of atoms/bonds in the structure (see Gushurst et. al. J. Chem. Inf. Comput. Sci., 1991, 31, 447-454).

The number n4 is an occurrence count counting the descriptor’s occurring “one or more” or up to “999 or more” times. The numbers n5-n9 in the keybit definition are used to control which keybits are set by the descriptor defined by the first four numbers. N5 is used to specify the number (1-3) of keybits which are set. N6 is a flag, 1 or 0, indicating whether or not the keybits are also set by other descriptors. The numbers n7-n9 identify the keybits.

An example is the following keybit:

Position:	n1	n2	n3	n4	n5	n6	n7	n8	n9
Key:	2	3	5	2	3	`	479	469	763

Here, there are at least two occurrences (n4) of an atom in a multiple, non-aromatic bond (n2) located two bonds (n1) away from an atom with at least two heteroatom neighbours (n3). The descriptor sets three keybits (n5), which can be set by other descriptors (n6). The keybits set are 479, 469, and 763 (n7-n9).

A few properties are incompatible, meaning that fewer descriptors are possible than are mathematically allowed. Also, a number of descriptors can be encoded in two different ways (e.g., by reversing n2 and n3) but the algorithm does not encode both options. Thus, 3234 different descriptors encoding occurrence counts of “one or more” are possible. Since occurrence counts up to “999 or more” are allowed, more than 3 million distinct descriptors can be combined into innumerable keysets. How does one select an optimum set of descriptors for use in molecular similarity calculations?

The authors tried to answer this question by adopting the success measure defined in Briem, H.; Lessel, U. Perspect. Drug Discovery Design 2000, 20, 231-244. This is calculated by taking the mean fraction of molecular nearest neighbours which are of the same activity class as the target active compound, and averaging this quantity over all active target compounds. Briem and Lessel’s data set, used by the MDL authors, contains 957 molecules from MDL Drug Data Report (MDDR), 383 of them in active In any one of 5 classes, and 574 inactive in those classes.

Briem and Lessel used Euclidean distances between keys; MDL used Hamming distance. In MDL’s genetic algorithm optimisations they made use of a “training set success measure”, rather than the one based on Briem and Lessel’s data set. The training set consisted of 1700 compounds from MDDR, belonging to 17 active classes, those classes being different from Briem and Lessel’s five.

Both the 166-bit and the 960-bit MDL keysets were used. The latter contains a number of keybits which can be set by more than one descriptor. If all the multiply mapped keybits are removed, a 726-bit keyset is left. Alternatively, each one of the descriptors encoded in the 960-bit keyset can be made to correspond to one unique keybit, yielding a 1387-bit keyset. The author also used a 3234-bit keyset formed by assigning unique keybit to each of the descriptors encoded by the underlying key setting algorithm, assigning an occurrence count to each descriptor of “set one or more times”.

Various approaches to optimisation are possible: steepest descent, information-theory based pruning (surprisal, and surprisal signal to noise ratio S/N), genetic algorithms, and humans using chemical insight. Optimisation is difficult because of the very high dimensional space, because the optimisation surface is very flat, and because there are many local minima.

Taylor showed the following plot for random pruning:

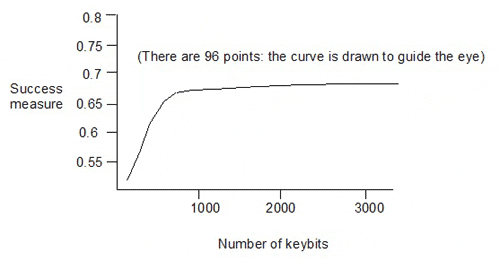
This gives the success measures for 96 keysets, with sizes from 100 to 3200 keybits, generated by eliminating descriptors from the 3234-bit keyset (in which each of the 3234 keybits corresponds to one of 3234 descriptors). The dependence of the success measure on the number of keybits is quite weak above about 1000 keybits in the keyset.

The published results of pruning the keybits from a keyset using surprisal or surprisal S/N ratio as the selection criterion are as follows:

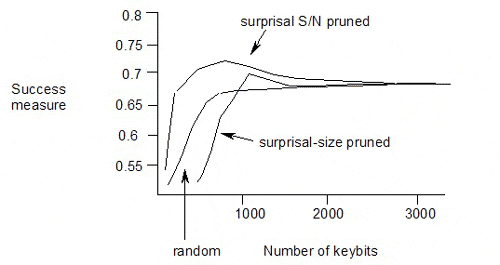
The maximum is at surprisal S/N of 1.9, with 711 keybits used in the keyset, and a success measure of 0.704.

The authors also pruned the 166-, 726-, 960- and 1387-bit keysets and plotted the success measure against the number of keys:

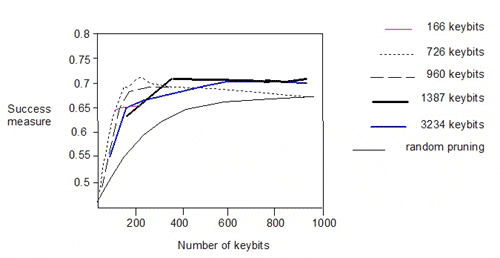
There is significant degradation in performance below 200 keybits. Interestingly, the performance of the 166-bit keyset lies on the curves for the 1387- and 3234-bit keysets. The similar performance of the various pruned keysets does not however, imply commonality in the descriptors encoded in the keysets.

In conclusion, MDL has produced keysets with optimised success measures up to 0.711 compared with success measures of 0.649 and 0.670 for the standard 166- and 960-bit keysets. Surprisal-based selection of keybits was found to be worse than random selection but surprisal S/N base selection outperformed random selection. The great insensitivity of overall performance on both keyset size and identity of the descriptors encoded resulted in great difficulty in optimising the performance using standard mathematical techniques. Genetic algorithm optimisation succeeded in producing keysets with better performance but MDL were not able to locate a single globally optimum keyset.

For hand optimisation, the authors took guidance from the GA and surprisal pruning results, and also considered the definitions of the 166 keys. They considered J. Med. Chem. articles by the Vertex group, showing that current drugs show relatively restricted diversity in terms of ring systems and sidechains. Finally, they gave priority to series descriptors, in which occurrence counts and bond distances varied systematically (e.g., 1, 2, 3 or more occurrences, and 2, 4, and 6 bonds), rather than randomly including particular members. This led to a selection of 324 keys that performed as well or better than the previously examined subsets.

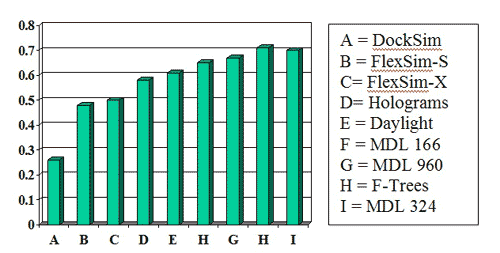
Success measures for the MDL 960-bit and 324-bit keysets were better than nearly all the other methods in two publications by Bemis and Murcko (J. Med. Chem. 1996, 39, 2887 and 1999, 42, 5095):

An experiment in differentiating toxics from drugs was carried out. A database was built by combining MDDR with MDL Toxicity: 141,012 structures were unique to MDDR, 110,138 structures were unique to MDL Toxicity and 1950 structures occurred in both databases. One hundred structures were selected at random. A search was carried out for structures 50% similar to these using weighted Tanimoto similarity. The hitlist size, percentage of hits in MDDR and percentage of hits in MDL Toxicity were recorded.

The authors were interested in the performance of the 324-keybit set compared to the 166- and 960-bit keysets from the standpoint of efficiency and relevance (i.e., does a weighted similarity search bring in a lot of hits, including irrelevant ones, or does it hit a select number of relevant structures). They measured hitlist size and percent MDDR structures of the given hitlist, using a 50% similarity search against 100 random query structures from MDDR, and using three types of weighting The resulting hitlist sizes for MDDR were as follows:

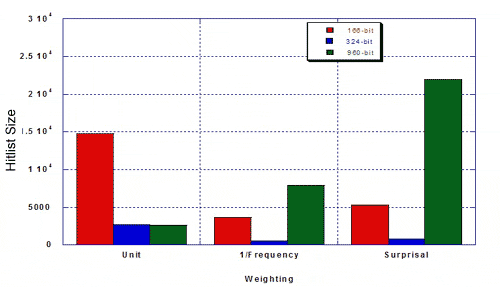
The percentage of true hits for MDDR was as follows.

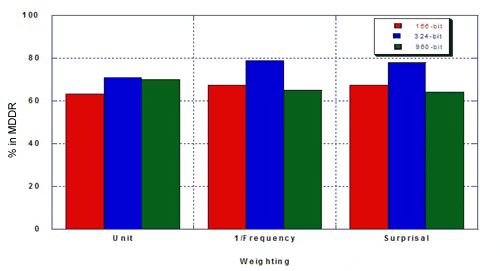
Taylor concluded that the re-optimised keyset outperformed existing 166- and 960-bit keysets: hitlists were more focused and there was a higher percentage of the desired class. Weighting improves the optimised keyset more than it improves existing 160- and 960-bit keysets. Key performance can be improved by re-optimising keysets. Key performance is not substantially improved for MDL keysets longer than about 500 bits. The hand-optimised keyset outperforms 166- and 960-bit keysets in differentiating structures in MDDR from structures in MDL Toxicity.

MDL keys can be accessed as an option in MDL ISIS/Host and the MDL Relational Chemistry Server databases but a structure must be registered. They can also be accessed through the MDL Chemistry Rules interface which takes an MDL molfile as input. In that case, registration into a database is not required. A 320- keybit set has now replaced the 324 keybit set discussed in this presentation. It is not “official”, results are not guaranteed, and the technology is under continuous refinement, but with these caveats, Taylor is willing supply a current version to interested parties.